I have DNA motifs represented by position-weight-matrices (PWMs) a.k.a position-specific scoring matrices (PSSMs), in transfac form (motif names are shown in rows following "DE", numbered rows represent the observed frequencies of letters along the sequence such that row 0 is the first letter along the sequence, the last column shows the most representative letter for that position along the sequence and these can be given ambiguity codes (not A,G,C,T) if no particular letter is representative:
DE SRF
0 0.0435 0.0217 0.8478 0.0870 G
1 0.1957 0.7174 0.0435 0.0435 C
2 0.0000 0.9782 0.0217 0.0000 C
3 0.0217 0.9782 0.0000 0.0000 C
4 0.6956 0.0217 0.0000 0.2826 A
5 0.0652 0.0217 0.0000 0.9130 T
6 1.0000 0.0000 0.0000 0.0000 A
7 0.0217 0.0000 0.0000 0.9782 T
8 0.9348 0.0000 0.0000 0.0652 A
9 0.3261 0.0217 0.0000 0.6522 T
10 0.0435 0.0000 0.9565 0.0000 G
11 0.0435 0.0217 0.9348 0.0000 G
XX
DE HMG-1
0 0.0000 0.3846 0.6154 0.0000 G
1 0.0000 0.0000 0.2308 0.7692 T
2 0.0000 0.3077 0.0000 0.6923 T
3 0.0000 0.1539 0.7692 0.0769 G
4 0.0000 0.0769 0.0000 0.9230 T
5 0.4615 0.0769 0.2308 0.2308 N
6 0.2308 0.3846 0.0000 0.3846 N
7 0.0000 0.0769 0.1539 0.7692 T
8 0.0000 0.6154 0.0769 0.3077 C
XXI would like to calculate the Shannon Entropy for each motif, could anybody advise me on how to do this? I am most comfortable with Python, so if you have a few lines of code available or can point me to some package that would let me do this, or even provide me with a formula that would be much appreciated.

 ,
, 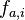 is the
is the  at position
at position 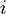

The mean of the entropy at each base is absolutely not the entropy of a motif. You're saying for example, a single BP with p=1/4 for atcg, has the same randomness as a ten BP sequence of such p=1/4's, when clearly the longer sequence contains more mathematical information. You asked a programming forum and copied the code from someone who added a disclaimer that he doesn't know what a biologists' entropy is.
@karl.stamm, Firstly I did not copy the code it's quite different, secondly I did check the StackOverflow post's formula against a source here and it completely agrees with the source, quoting the source: " , where
, where 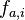 is the relative frequency of base or amino acid
is the relative frequency of base or amino acid  at position
at position 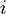 " ...The person who posted from StackOverflow made one assumption, which is coincidentally the pivotal assumption that profile hidden-markov model-based DNA profile alignment models make.
" ...The person who posted from StackOverflow made one assumption, which is coincidentally the pivotal assumption that profile hidden-markov model-based DNA profile alignment models make.
Everything has an
isubscript. This formula is correct as a per-base entropy, but that's irrelevant for the motif. Consider a motif of fifty As and one 25%-anything base. There's clearly only four possibilities, all equally likely, but the mean of 51 entropies will be nearly zero. Being a uniform distribution, this should have the highest entropy, and H=2 bits at the 25%-anything base, but do you mean for it to be averaged with the constant bases? Under my model of using all possible sequences, the constant bases don't impact the motif entropy, but under your model, fifty As will drown out the signal. I guess it depends on your requirements, but I need to insist that a mean ofH sub iis not the entropy of a motif.You sound quite convincing, which makes me feel you're onto something, but I can't quite understand what you're saying... which probably means I've some more reading to do, so cheers.